abs
|
Absolute value
|
Computes the absolute value of its argument. This is completely equivalent to using the absolute value bars. So, abs(3-7) = |3 – 7|=4.
|
ceiling
|
ceiling (opposite of “floor)”
|
Returns the closest integer greater than or equal to its argument: ceiling (7.3) returns 8.
|
combinations
|
combinations(n, k)
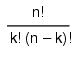
|
Returns the number of combinations of n things taken k at a time. For example, combinations(5,2) is 10.
|
exp
|
Exponential function (“e to the…”)
|
Raises e, the base of the natural logarithms, to a power: exp(2) is about 7.34; exp(1)is e, which is 2.718….
|
floor
|
Sometimes written using
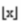 , where x is the number whose floor you want , where x is the number whose floor you want
|
Returns the closest integer less than or equal to its argument: floor(3.98) is 3; floor(–3.98) is –4.
|
gcd
|
Greatest common divisor (greatest common factor)
|
Returns the largest positive integer that divides its integer arguments without a remainder. For example, gcd(8,12) is 4. Returns an error if either of its arguments is not a positive integer.
|
ln
|
Natural logarithm
|
Returns the number, which, used as the power of e, gives the argument. For example, ln(12) is about 2.485 because e^2.485 is about 12.
|
log
|
Common logarithm
|
Returns the number, which, used as the power of 10 gives the argument. For example, log(1000) is 3 because 10^3 is 1000.
|
logRelativeError
|
Returns, roughly, the number of digits in agreement between the two arguments
|
logRelativeError(expected, actual) is defined as -log(|actual-expected|/expected). With the arguments 1.0 and 1.01, the result is 2 because there are two digits in common.
|
modulo
|
Often written as “mod” as in 7 mod 3 = 1
|
Returns the modulus, the remainder after one number is divided by another: modulo(11, 4) is 3. The numbers need not be integers: modulo(12.1,1.5) is 0.1.
|
round
|
Rounds to the nearest integer
|
This function has an optional, second argument that specifies how many decimals to round to: round(3.14) is 3, round(π, 4) is 3.1416, and round(1234, –2) is 1200.
|
scalar
|
Takes a quantity (number with units) and returns just the number
|
Use this when you need to get rid of the units: scalar(7s) is 7. Be aware that changing units of an attribute will affect the value that scalar returns.
|
sgn
|
Signum function
|
Returns +1 for arguments > 0; –1 for arguments < 0; 0 for arguments = 0.
|
sqrt
|
Square root function
|
Examples: sqrt(4) returns 2; sqrt(9m^2) returns 3 m.
|
trunc
|
Truncation function
|
Returns the integer part of the argument: trunc(3.1415) returns 3; trunc(-1.234) returns –1.
|
unitOf
|
Returns a quantity with the numeric value of 1 and the units of its argument
|
Examples: unitOf(8years) returns 1 year; unitOf(3m/s * 2s) returns 1 m.
|





